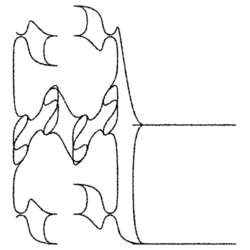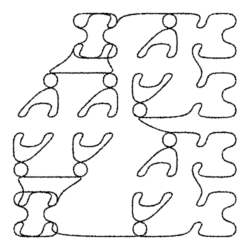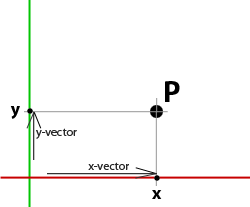
Figure 1
Although these vectors represent the x and y coordinates of P, like any vector, they have their own coordinates. For example, the coordinates of the x-vector (in two dimensions) might be [1,0] while the coordinates of the y-vector might be [0,0.5]. To prevent the confusion of labelling the coordinates of these vectors as "x" and "y" they are instead labelled "i" and "j". For example,
x-vector y-vector
xi = 1.0 yi = 0.0
xj = 0.0 yj = 0.5
We can make use of these vectors to move (ie. translate) a copy of point P. For example, in Andrew's procedure we see this statement.
LineTo(x + (xi + yi)/2, y + (xj + yj)/2);
Rewritten for point P we have,
Px = Px + (xi + yi)/2
= 1.0 + (1.0 + 0)/2
= 1.5
Py = Py + (xj + yj)/2
= 0.5 + (0 + 0.5)/2
= 0.75
The effect of using the i's and j's on point P can be seen in figure 2.
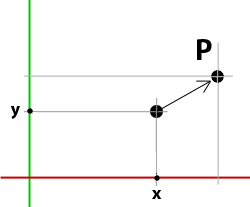
Figure 2
Point P could also have been translated by directly changing its x and y values. However, using the "i" and "j" coordinates (x-vector and y-vectors) moves the point in a structured and proportional fashion. In the context of their use in Andrew's procedure, the "i" and "j" components provide, what are in effect, additional "handles" to control the placement of points along the Hilbert curve.