Mel
Align Y Axis to Vector

return to main index

Introduction

Occasionally it is necessary to apply a series of rotations to a coordinate system so that one of its axes points in a specific direction. This tutorial explains how the y-axis of a coordinate system can be aligned to a direction specified by a vector.

Although the calculations shown on this page were derived from "The RenderMan Companion" by Steve Upstill (pages 142/143) I have altered them slightly because RenderMan uses a left-hand coordinate system whereas Maya uses a right hand system. An additional difference between Upstill's calculations and mine is that his code transforms the (RenderMan) camera coordinate system.

Despite these differences the method by which a coordinate system is transformed is essentially the same in both Upstill's "AimZ" function and my "AimY" procedure. If you have studied Upstills code and have wondered why his calculations work I hope the illustrations on this page makes the mathematics he uses a little clearer.

Coordinate Axes

Fig 1 shows a vector with coordinates [-2,2,1]. The pale red trace lines show the vector projected onto the x-y plane, the x-z plane and the y-z plane. The easiest way of figuring out how to rotate the coordinate system so that the y-axis points in the direction of the vector is to think about the problem in reverse! How can the vector be aligned to the current y-axis. The vector in question is shown below in black - coordinates [-2, 2, 1].

Figure 1

Rotations

Step 1

Figure 2 shows the vector forms the hypotenuse a right angled triangle.

Step 2

Figure 3 shows the triangle can be aligned to the y-z plane by applying a suitable rotation around the z-axis.

Figure 2 - vector forms a triangle

Figure 3 - rotation around the z-axis

Step 3

Fig 3 shows that a rotation around the x-axis will align the vector to the y-axis of the coordinate system (fig 4).

Figure 4 - rotation around the x-axis

Figure 5 - vector aligned with the y-axis

Angles

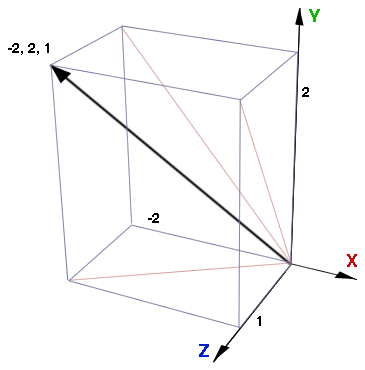
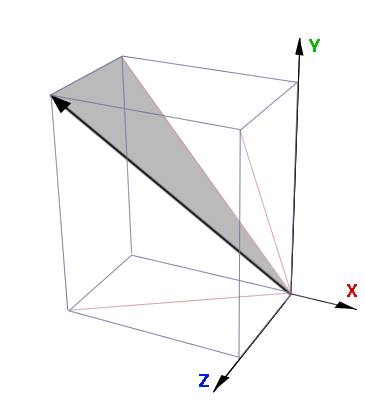
Figure 6 shows two angles that must be calculated in order to perform steps 2 and 3. To find the blue angle we must first calculate the length of the red trace line, xyLength, on the x-y plane ie.

Figure 6 - the two principle angles

    xyLength = sqrt(x * x + y * y);
    xyLength = sqrt(-2 * -2 + 2 * 2);
    xyLength = 2.83;

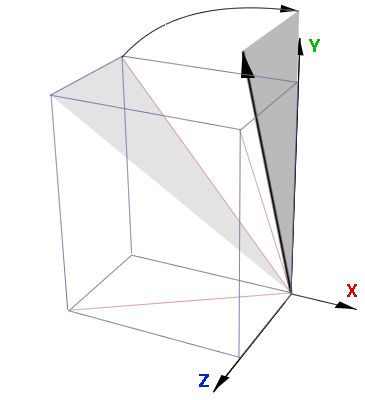
After which the angle shown in blue can be found,

    zAngle = acos(y / xyLength);
    zAngle = acos(2.0 / 2.83);
    zAngle = 0.785;	/* acos returns angle in radians */

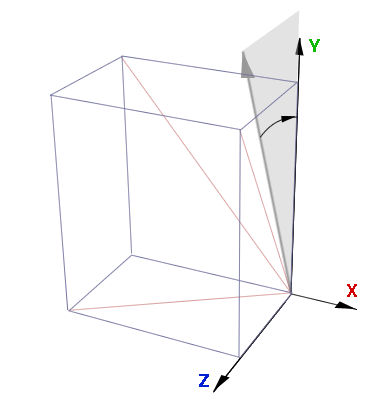
To find the dark gray angle the length of the vector must be found,

    vecLength = sqrt(x * x + y * y + z * z);
    vecLength = sqrt(-2 * -2 + 2 * 2 + 1 * 1);
    vecLength = 3.0;

As with the blue angle the angle in dark gray is found from the cosine. I am referring to this angle as the xAngle because, as shown in Fig 4, this angle will be used to define the rotation around the x-axis.

    xAngle = acos(xyLength / vecLength);
    xAngle = acos(2.83 / 3.0);
    xAngle = 0.338;

Expressed in degrees the zAngle is 45.0 and the xAngle is 19.4. Therefore, the rotations needed to orientate the y-axis in the direction of the vector requires,

1. a rotation around the x-axis of 19.4 degrees, then,
2. a rotation around the z-axis of -45 degrees

A mel procedure that implements this technique is given in listing 1.

Listing 1

proc float[] aimY(vector $vec)
{
float $out[2];
float $xAngle, $zAngle, $xyLength, $vecLength;
  
$xyLength = sqrt(($vec.x) * ($vec.x) +
                  ($vec.y) * ($vec.y));
$vecLength = sqrt(($vec.x) * ($vec.x) +
                   ($vec.y) * ($vec.y) + 
                   ($vec.z) * ($vec.z));
  
// $xyLength will be zero when $vec is pointing
// along the +z or -z axis
if($xyLength == 0)
    $zAngle = ($vec.x) > 0 ? deg_to_rad(90) : deg_to_rad(-90);
else
    $zAngle = acos(($vec.y)/$xyLength);
  
$xAngle = acos($xyLength/$vecLength);
  
$xAngle = ($vec.z) > 0 ? $xAngle : -$xAngle;
$out[0] = rad_to_deg($xAngle);
  
$zAngle = ($vec.x) > 0 ? -$zAngle : $zAngle;
$out[1] = rad_to_deg($zAngle);
return $out;
}

Checking the Script

The following script uses the aimY() procedure to point a cone along a vector. Fig 7 shows that the apex of the cone does extend along the vector - the coordinates of which are indicated by the gray box.

Figure 7 - a cone aligned to a direction vector

    vector $v = <<-2,2,1>>;
    float $a[] = aimY($v);
      
    // begin with an empty scene 
    select -all;
    delete;
      
    // insert a cone aligned to the y-axis
    cone -r 0.2 -hr 17 -ax 0 1 0;
      
    // apply the rotations to the x 
    // and z axes of the cone
    rotate -r $a[0] 0  0;
    rotate -r 0     0  $a[1];
      
    // draw a box to indicate the coordinates of the vector
    polyCube -w  2 -h 2 -d 1;
    move -r -1 1 0.5;