Mel - Recursion & Branching

Mel
Recursion & Branching

Introduction

This tutorial develops a practical application of recursion to generate shapes that resemble trees. The recursive procedure tree() (listing 1) presented in this tutorial produces two branches at each node. The procedure uses the following algorithm to find the end points of the branches that extend in a growthDir vector.

Finding the First Branch

Given growthDir, branchAngle and branchLen,

1 Calculate a circle representing the branch radius - figure 1.
2 Find a random vector on the circle - figure 2.
3 Translate the vector up the y-axis by branch length units - figure 3.
4 Rotate the vector by the branch angle to find the end of a branch - figure 4.
5 Draw a line between the base of the branch and the (relative) end of the branch.
6 Recurse

Figure 1

	Figure 2		Figure 3
	Figure 4

Finding the Second Branch

Given growthDir, branchAngle and a vector defining the first branch
1 Define the second branch as if it were a reflection of the first
branch about the growthDir vector - figure 5,
2 Move the end of the second branch relative to the base point,
3 Draw the second branch,
4 Recurse

Figure 5

	Sample Trees
	Figure 6		Figure 7

Listing 1 (tree.mel)

//==============================================
//    aimY
//==============================================
proc float[] aimY(vector $vec)
{
float $out[2];
float $xAngle;
float $zAngle;
float $xyLength;
float $vecLength;
  
$xyLength = sqrt(($vec.x) * ($vec.x) +
                ($vec.y) * ($vec.y));
$vecLength = sqrt(($vec.x) * ($vec.x) +
                ($vec.y) * ($vec.y) + 
                ($vec.z) * ($vec.z));
  
// $xyLength will be zero when $vec is pointing
// along the +z or -z axis
if($xyLength == 0)
    $zAngle = ($vec.x) > 0 ? deg_to_rad(90) : deg_to_rad(-90);
else
    $zAngle = acos(($vec.y)/$xyLength);
  
$xAngle = acos($xyLength/$vecLength);
  
$xAngle = ($vec.z) > 0 ? $xAngle : -$xAngle;
$out[0] = rad_to_deg($xAngle);
 
$zAngle = ($vec.x) > 0 ? -$zAngle : $zAngle;
$out[1] = rad_to_deg($zAngle);
return $out;
}
  
//==============================================
//    vectorOnCircle
//==============================================
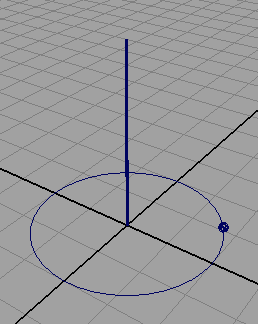
proc vector vectorOnCircle(float $rad)
{
// find a random vector within a 2 * rad square
float $x = rand(-$rad, $rad);
float $y = 0;
float $z = rand(-$rad, $rad);
vector $vec = <<$x, $y, $z>>;
  
// convert to a unit vector - this will place
// head of the vector on a circle of radius 1
$vec = unit($vec);
  
// scale it by $rad
$vec = $vec * $rad;
return $vec;
}
  
//==============================================
//    reflect
//==============================================
proc vector reflect(vector $i, vector $n)
{
$i = unit($i);
$n = unit($n);
return $i - 2 * dot($i, $n) * $n;
}
  
//==============================================
//    tree
//==============================================
proc tree(int     $depth,
        vector    $base,
        vector    $growthDir, 
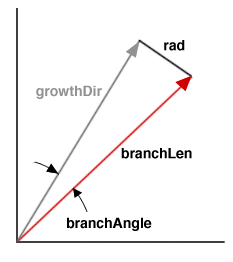
        float     $branchAngle,
        float     $branchLen)
{
if($depth <= 0)
    return;
    
// STEP 1 Find the size of a circle such that if it was
// located at the end of the branch it would define
// a cone whose apex angle equals twice the "branchAngle".
$rad = $branchLen * sin(deg_to_rad($branchAngle));
  
// STEP 1.1    Randomly choose a point on a circle
vector $vec = vectorOnCircle($rad);
  
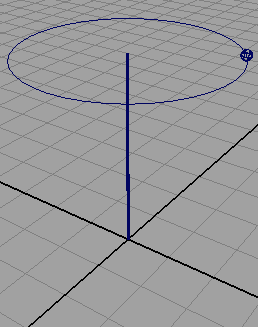
// STEP 1.2 Transform the point on the circle so that 
// its "branchLen" units up the world y-axis
vector  $x_axis = <<1,0,0>>;
vector  $y_axis = <<0,1,0>>;
vector  $z_axis = <<0,0,1>>;
$vec = $vec + <<0, $branchLen, 0>>;
  
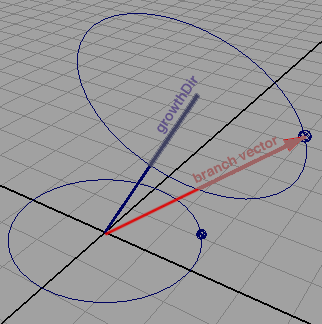
// STEP 1.3 Find the x-axis/z-axis rotations that will
// align the branch $vec to the "growthDir".
float $angle[2] = aimY($growthDir);
$vec = rot($vec, $x_axis, deg_to_rad($angle[0]));
$vec = rot($vec, $z_axis, deg_to_rad($angle[1]));
  
$vec = <<($vec.x), ($vec.y), ($vec.z)>>;
  
// STEP 1.4 Locate the end of the branch relative to the
// base of the branch.
vector $end1 = $base + $vec;
  
// STEP 1.5 Finally, draw the curve segment that "represents"
// the first branch.
curve -d 1  -p ($base.x) ($base.y) ($base.z)
            -p ($end1.x) ($end1.y) ($end1.z);
  
// Recurse to the next branch
tree($depth - 1, $end1, $vec, $branchAngle, $branchLen * 0.6);
  
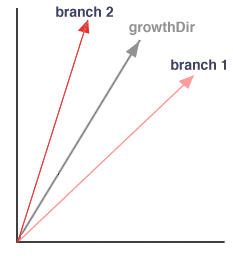
// STEP 2 Define the second branch as if it were a 
// reflection of the first branch first about the "growthDir"
$vec = reflect(-$vec, $growthDir);
  
$vec = <<($vec.x), ($vec.y), ($vec.z)>>;
  
// STEP 2.1 Locate the end of the branch relative to the
// base of the branch.
vector $end2 = $base + $vec;
  
// STEP 2.2 Finally, draw the curve segment that "represents"
// the second branch.
curve -d 1  -p ($base.x) ($base.y) ($base.z)
            -p ($end2.x) ($end2.y) ($end2.z);
  
// Recurse to the next branch
tree($depth - 1, $end2, $vec, $branchAngle, $branchLen * 0.6);
}
  
select -all;
delete;
  
//seed(1);
vector $begin = <<0,0,0>>;
vector $dir = <<0,1,0>>;
float $angle = 13;
float $len = 2;
tree(7, $begin, $dir, $angle, $len);