OSL
Regular Polygon

return to main index

Introduction

This tutorial presents a relatiely simple way of drawing a regular polgon with any number of sides (greater than two). Figure 1 illustrates the approach which is based on the observation that the distance (dist) of a point (P0) to the red edge of the polygon is the same when P0 and the edge are rotated so that the edge is aligned to the "vertical" axis. If the radius of the inscribed circle of the polygon is known, it is trivial to calculate the distance of P1 to the rotated edge - shown below in blue.

Evaluating the distance based on the x-difference is faster than calculating the distance using a "point-to-line" function - refer to the tutorial "Vectors: Shortest Distance from a Point to a Line".

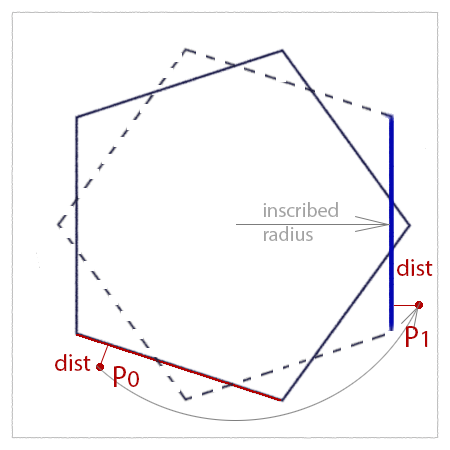
Figure 1

To calculate the angle required to rotate the red line to the blue line we must know the "segment" in which point P0 is located. For example, figure 2 shows a regular pentagon consisting of 5 "segments" each of which have an interior angle of 72 degrees (360/5).

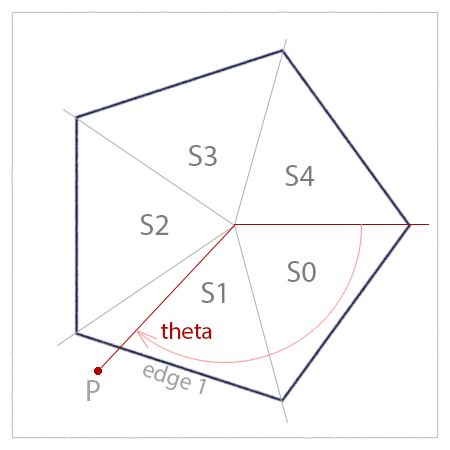
Figure 2

For the purpose of illustration point P defined by its polar coordinate of theta. Assuming theta is, say, 125 degrees then dividing it by the "interior" angle of 72 degrees gives a value of 1.74 which, after rounding down, indicates that P is "in" segment 1.

    interior_angle = 360.0 / number of sides
    segment = floor(theta / interior_angle)
    segment = floor(125.0 / 72.0)
    segment = 1

Because P is "in" segment 1 the angle required to rotate "edge 1" is,

    rotation = segment * interior angle + half_interior_angle
    rotation = 1 x 72 + 36 degrees
    rotation = 108 degrees

If the 'st' coordinates of P0 are,

    s = 0.2
    t = 0.9

then its coordinates after rotation (P1) will be,

    s = 0.92
    t = 0.68

If the size of the polygon is defined by its inscribed radius, say, 0.35, then the distance of P to edge 1 (figure 2) is,

    dist = abs(inscribed_radius - P1.s)
    dist = abs(0.35 - 0.68) 
    dist = 0.33

If the distance is less than the thickness of the polgon edge then P should receive the foreground color, otherwise, it should be assigned the background color.

Listing 1 - polygon.osl

shader
polygon( float numSides = 4,
         float innerRad = 0.25,
         float line = 0.02,
         color bkcolor = 1,
         color frcolor = color(0, 0, 0.2),
         float s = 0  [[ int lockgeom = 0, string widget = "null" ]],
         float t = 0  [[ int lockgeom = 0, string widget = "null" ]],
        output color resultRGB = 0)
{
// 1   Convert the current 'st' to polar coordinates
//     Note: positive theta is clockwise.
float   x = s - 0.5, y = t - 0.5;
float   theta = atan2(y, x); // -PI to PI radians
if(theta < 0.0)
    theta += 2 * M_PI;        //  0 to 2PI radians
  
// 2   Find the "seqment" in which the current shading point is located.
float interior = (2 * M_PI)/numSides;
float seqment = floor(theta/interior);
  
// 3   Find the angle to (counter) rotate the current shading point. 
//     Note: positive rotation is anti-clockwise.
float rotation = (seqment * interior + interior/2);
  
// 4   Apply the rotation to a 3D point defined by the uv location. 
point  stPnt = point(s - 0.5, 0.5 - t, 0);
point  origin = point(0, 0, 0);
point  z_axis = point(0, 0, 1);
point  rotPnt = rotate(stPnt, rotation, origin, z_axis);
  
// 5   Use the x component of the rotated point to determine the 
//     "proximity" of the current shading point to a polygon edge.
//       Using the smoothstep function twice ensures "proximity" is in 
//     the range 0.0 to 1.0.
float proximity = smoothstep(innerRad - line/2, innerRad, rotPnt[0]) *
              (1 - smoothstep(innerRad, innerRad + line/2, rotPnt[0]));
  
// 6   Finally, use "proximity" to output the appropriate color.       
resultRGB = mix(bkcolor, frcolor, proximity);
}