Rsl - Using Noise

RSL
Using noise

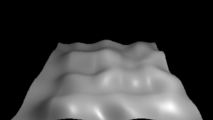
Variety

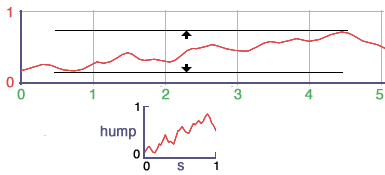
The shading language incorporates many useful maths functions that can be used to generate visual effects such as bumpiness and variations in color. Maths functions, however, produce visual effects that look unnaturally smooth and regular. The noise() function can be used to add variations to a visual effect. The noise function can be considered to be a black-box number generator. Irrespective of the magnitude of its inputs, the output values from the noise() function are, in theory, always in the range 0 to 1. In practice the output values are generally in the range 0.27 to 0.7.

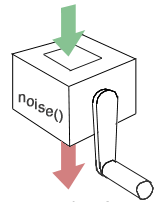
Figure 1 - the "noise" machine!

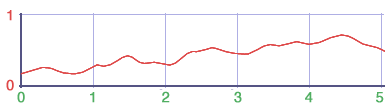
Figure 2 - a plot of noise values

Frequency & Amplitude

In a displacement shader noise might be used to effect the bumpiness of a surface in say the 's' direction, for example,

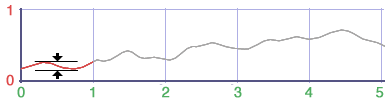
plot2
Figure 3

Because the default values of 's' range from 0 to 1 the resulting frequency of the noise is low. This can been seen in figure 3 where there is only a couple of peaks and valleys along the first part of the line segment. A poly plane displaced by,

    hump = noise(s);

is shown in figure 4.

Figure 4

Figure 5

To increase the frequency of the output values (from the noise function) the input values are scaled, for example,

plot3

A poly plane displaced by,

    hump = noise(s * 5);

is shown in figure 5. To control the amplitude of the noise its output value can be scaled. In the line of code shown below the difference in height between the valleys and peaks is reduced by approximately a third ie.

    hump = noise(s * 5) * 0.3;

Figures 4 and 5 are examples of one-dimensional noise.

2D Noise

The noise() function also accepts two input values, for example,

    hump = noise(s * 5, t * 5) * 0.3;

Using two values generates two-dimensional noise.

Figure 6

Listing 1 shows that replacing the constant values (5 and 0.3) with the instance variables, freq and amp, makes the shader more flexible because those parameters can be set in the rib file.

Listing 1

displacement
basic_2d_noise(float Km = 0.1,
                     freq = 5,
                     amp = 1)
{
float  hump = 0;
point  n = normalize(N);
            
hump = noise(s * freq, t * freq) * amp;
                    
P = P - n * hump * Km;
N = calculatenormal(P);
}

3D Noise

The noise function also accepts a three-dimensional input. For example, we could use the global variable P that references the xyz coordinates of the point that is currently being displaced by a shader.

Figure 7

Listing 2

displacement
basic_3d_noise(float Km = 0.1,
                     freq = 5,
                     amp = 1)
{
float  hump = 0;
point  n = normalize(N);
  
hump = noise(P * freq) * amp;
  
P = P - n * hump * Km;
N = calculatenormal(P);
}

Sticky 3D Noise

A problem arises when using the global variable P as a source of data because its xyz coordinates are, by default, measured relative to the camera. In other words, P is in the camera coordinate system. Therefore, changing the distance or orientation of the world relative to camera causes the surface to appear to slide over stationary bumps. Three frames of an animation are shown in figure 8. Note that despite the rotation of the polyplane the "feature" shown in red remains fixed in the same position relative to the picture frame. In other words the noise is, in effect, parented to the camera!

Figure 8

Figure 9

To make the displacements "stick" to the surface of the polyplane, point P should not be used directly but instead a copy of its data, transformed into "object" or "shader" (coordinate system) space, is used instead. Listing 3 gives an example of how this is accomplished.

Listing 3

displacement
parented_3d_noise(float Km = 0.1,
                      freq = 5,
                      amp = 1;
               string space = "object")
{
float  hump = 0;
point  n = normalize(N),
pp = transform(space, P);
  
hump = noise(pp * freq) * amp;
  
P = P - n * hump * Km;
N = calculatenormal(P);
}