RSL
Repeating Patterns

return to main index

Introduction

The shading language functions mod() and floor() are used to generate repeating patterns. The displacement pattern shown in figure 1 is based on the smoothbump3.sl shader developed in the tutorial "Using Smoothstep". A slightly modified version of its source code is shown below.

Listing 1

float square(float x,y,minx,maxx,miny,maxy,taper)
{
return smoothstep(minx, minx + taper, x) *
        (1 - smoothstep(maxx, maxx + taper, x)) *
        smoothstep(miny, miny + taper, y) *
       (1 - smoothstep(maxy, maxy + taper, y));
}
            
displacement 
basicbump(float   Km = 0.1,
                  min_s = 0.1, max_s = 0.8,
                  min_t = 0.1, max_t = 0.8,
                  blur = 0.1)
{
float    hump = 0;
normal   n = normalize(N);
  
hump =  square(s, t, min_s, max_s, min_t, max_t, blur);
  
P = P - n * hump * Km;
N = calculatenormal(P);
}

Figure 1 - a smoothsteped square displacement

What is the mod() Function

The mod() function divides one number by another but returns only the remainder. For example,

    mod(3, 2);

returns the value 0.5 - the remainder of 3 divided by 2. The function can be used to map the range 0 to 1 to a sequence of repeating sub-ranges 0 to 1. In each sub-range the maximum value becomes infinitly close to 1 but never actually reaches that value.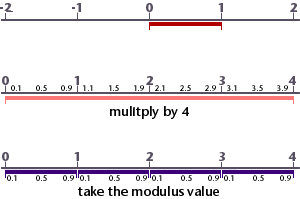

The mod() function is useful when creating repeating patterns on a surface.

Figure 2 - 4x4 repeating pattern

To generate 8 repeating patterns, say in the 's' direction, the following expression could be applied.

    float ss = mod(s * 8, 1);

Using 1 as the divider ensures we obtain the correct remainder. The effect of using mod() in both 's' and 't', with a repetition of 4, is shown in figure 2..

Using the mod() Function

The "repeatbump" shader shown in listing 1 is a slightly modified version of the previous "basicbump" shader. For brevity the code for the function "square" is not shown. Only the new code is shown colored, the original code is shown in gray. Download repeatbump.sl

Listing 2

displacement
repeatbump(float    Km = 0.1,
                    min_s = 0.1, max_s = 0.8,
                    min_t = 0.1, max_t = 0.8,
                    blur = 0.1,
                    s_repeats = 4, t_repeats = 4)
{
float    hump = 0;
normal   n = normalize(N);
  
float ss = mod(s * s_repeats, 1);
float tt = mod(t * t_repeats, 1);
hump =  square(ss, tt, min_s, max_s, min_t, max_t, blur);

P = P - n * hump * Km;
N = calculatenormal(P);
}

Using the floor() Function

The floor() function returns the integer portion of a number. For example, floor(3.7) returns 3. As such it can be used to determine which part of the repeat pattern our shader is currently being used on. Listing 3 provides the code that generated the staggered repeats seen in figure 3.

Listing 3

displacement
staggeredbump(float Km = 0.1,
                    min_s = 0.1, max_s = 0.8,
                    min_t = 0.1, max_t = 0.8,
                    blur = 0.1,
                    s_repeats = 4, t_repeats = 4)
{
float    hump = 0;
normal   n = normalize(N);
  
float ss = mod(s * s_repeats, 1);
float tt = mod(t * t_repeats, 1);
float row = floor(t * t_repeats);
  
/* Move "even" rows over 50% and then calculate ss */
if(mod(row, 2) == 0)
    ss = mod((s + 0.5) * s_repeats, 1);
  
hump =  square(ss, tt, min_s, max_s, min_t, max_t, blur);
P = P - n * hump * Km;
N = calculatenormal(P);
}

Figure 4

To see how this is done with a surface color refer to staggeredcolor.sl. For a highly detailed explanation about patterns refer to,

    Texturing & Modeling - A Procedural Approach by
    Ebert, Musgrave, Peachey, Perlin and Worley
    Morgan Kaufman Publishers
    ISBN: 1-55860-848-6