Introduction
The python scripts presented in this tutorial generate Sierpinski gaskets rendered
as RenderMan "Points" and "Blobby's". The python code was a direct port from the
RSL code presented in the tutorial
RSL: Sierpinski Point Clouds. The technique used
by both tutorials is taken from,
Fractals for the Classroom
by Maletsky, Perciante and Yunker
ISBN: 0-387-97041-X
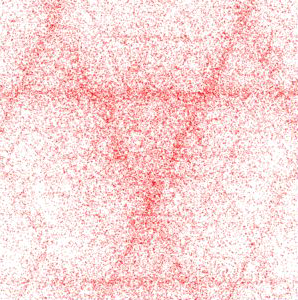
As shown below, the progressive build up of points in a Sierpinski gasket occurs
randomly. A slightly modified version of the python script "sierpinski.py" (listing 1)
was used to generate the 2D cloud of points. Instead of specifying four points, the
modified script only provided three ie.
inputs = [ [0,0,1], [1,0,-1], [-1,0,-1] ] #, [0,1.5,-0.2] ]
Listing 1 (sierpinski.py)
# A RenderMan procedural primitive that outputs a Sierpinski
# gasket as a RenderMan Points (RiPoints) primitive.
import math, random, sys
# Returns a point midway between point "p1" and point "p2"
def halfStep(p1, p2):
x = (p2[0] - p1[0]) / 2
y = (p2[1] - p1[1]) / 2
z = (p2[2] - p1[2]) / 2
result = [p1[0] + x, p1[1] + y, p1[2] + z]
return result
# Randomly chooses a point from a list of points
def pickVert(listOfPnts):
numPnts = len(listOfPnts)
index = math.floor(random.random() * numPnts);
return listOfPnts[int(index)]
args = sys.stdin.readline()
while args:
arg = args.split()
pixels = float(arg[0]) # this is ignored
numpnts = int(arg[1]) # number of points to generate
dia = float(arg[2]) # the "width" of each point
# The points define the tetrahedron that will bound
# the sierpinski gasket.
inputs = [ [0,0,1], [1,0,-1], [-1,0,-1], [0,1.5,-0.2] ]
# An arbitary seed point
playpnt = [0.0, 0.5, 0.0]
print('Points "P" [\n') # Begin the "Points" primitive
for n in range(numpnts):
pnt = pickVert(inputs)
playpnt = halfStep(playpnt, pnt)
print('%1.3f %1.3f %1.3f\n' % (playpnt[0], playpnt[1], playpnt[2]))
print('] "constantwidth" [%f]\n' % dia)
sys.stdout.write('\377')
sys.stdout.flush()
args = sys.stdin.readline() # read the next set of inputs
|
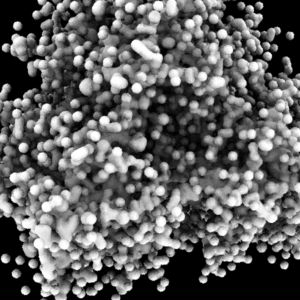
Listing 2 is a rib file that uses the unmodified version of the sierpinski.py script to generate a 3D Sierpinski gasket - figure 2.