OSL - Repeating Patterns

OSL
Repeating Patterns

Introduction

For the purpose of illustrating how repeating patterns are generated the code shown in listing 1 will be modified so that it produces not just one square, figure 1, but many squares, figure 2.

Figure 1

Figure 2

Listing 1

// Returns a value in the range 0 to 1.
// 0 indicates the x,y point is outside the square, and
// 1 indicates the x,y point is fully within the squere. 
float pntInSquare(float x,
                  float y,
                  float x_center,
                  float y_center,
                  float x_width,
                  float y_width,
                  float blur)
{
float minx = x_center - x_width/2;
float maxx = x_center + x_width/2;
float miny = y_center - y_width/2;
float maxy = y_center + y_width/2;
  
return smoothstep(minx, minx + blur, x) * (1 - smoothstep(maxx, maxx + blur, x)) *
       smoothstep(miny, miny + blur, y) * (1 - smoothstep(maxy, maxy + blur, y));
}
//----------------------------------------------------        
shader 
square(float   s_center = 0.5, 
       float   t_center = 0.5,
       float   s_width = 0.4, 
       float   t_width = 0.4,
       float   blur = 0.01,
       color   bakcolor = 1,
       color   patcolor = 0,
       float   s = 0 [[int lockgeom = 0]],
       float   t = 0 [[int lockgeom = 0]],
    output color resultRGB = 0)
{
float blend = pntInSquare(s, t, s_center, t_center, s_width, t_width, blur);
resultRGB = mix(bakcolor, patcolor, blend);
}

Repetitions

Repetitions are based on the use of the mod() function. The function divides one number by another and returns the remainder. For example,

    mod(3, 2);

returns the value 0.5 - the remainder of 3 divided by 2. The function can be used to remap values in the range 0 to 1 to a sequence of repeating sub-ranges. In each sub-range the maximum value becomes infinitly close to 1 but never actually reaches that value.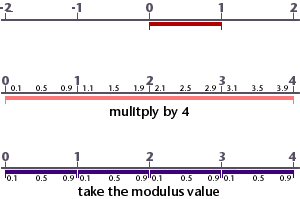

To generate 8 repeating patterns, say in the 's' direction, the following expression could be applied.

    float ss = mod(s * number_of_repeats, 1);

Using 1 as the divider ensures we obtain the correct remainder. The effect of using mod() in both 's' and 't', with a repetition of 8, is shown in figure 2..

Modifying the "square" shader, listing 1, so that it can render repeating squares is just a matter of passing remapped versions of 's' and 't' to the pntInSquare() function. For example,

    float ss = mod(s * number_of_repeats, 1);
    float tt = mod(t * number_of_repeats, 1);
    float blend = pntInSquare(ss, tt, s_center, t_center, s_width, t_width, blur);

The full code of a "squares" shader is shown in listing 2.

Listing 2

shader 
squares(float   s_center = 0.5, 
        float   t_center = 0.5,
        float   s_width = 0.4, 
        float   t_width = 0.4,
        float   blur = 0.01,
        color   bakcolor = 1,
        color   patcolor = color(0,0,0.2),
        float   s_repeats = 8,
        float   t_repeats = 8,
        float   s = 0 [[int lockgeom = 0]],
        float   t = 0 [[int lockgeom = 0]],
    output color resultRGB = 0)
{
float ss = mod(s * s_repeats, 1);
float tt = mod(t * t_repeats, 1);
  
float blend = pntInSquare(ss, tt, s_center, t_center, s_width, t_width, blur);
resultRGB = mix(bakcolor, patcolor, blend);
}