Figure 1
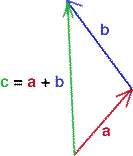
Figure 2
Vectors
|
Introduction
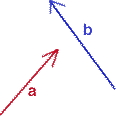
Vectors are entities that have direction
and length ie. magnitude. Typically, they are defined by 2
or 3 values. Part of the confusion in dealing with vectors is the way
they are represented in illustrations. Often they are represented
as free vectors that can be moved into arbitary locations
depending on the concept that is being explained.
|
|
|
|
|
Figure 1 shows two free vectors, c = a + b
where a, b and c are vectors. |
Fixed Vectors
When considering certain mathematical operations
on vectors it is essential to be aware that vectors are not "free"
but are fixed at the origin of a coordinate system. For example, although it makes
visual sense to show a surface normal (a type of vector) extending
directly from, say a polygon, the normal is not located at the
surface of the polygon but is located at the origin of
the coordinate system in which the polygon is defined and as such the vector
must be treated as fixed vector.
cx = ax + bx cy = ay + by
For vector subtraction, again, the result is another vector.
To find the coordinates of the resulting vector the corresponding components
are subtracted ie. cx = ax - bx cy = ay - by
Always keep in mind when it comes to arithmetic, vectors are fixed and as such their "tails" are "anchored" to the origin of the coordinate system. |
© 2002- Malcolm Kesson. All rights reserved.