Vectors
Shortest Distance from a Point to a Line

return to main index

Introduction

This tutorial presents a relatively straight forward explanation of how the shortest distance between a point and a line can be calculated. Readers who have searched the internet for information on this topic know there is no shortage of confusing, and often confused, "explanations" about point-to-line calculations.

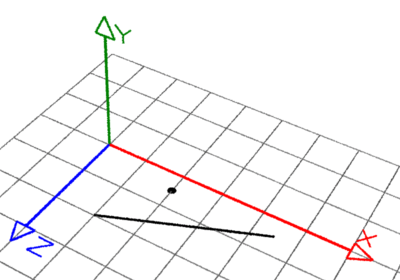
Computer graphics typically deals with lines in 3D space as those defined by points that provide the coordinates of the start and end of a line. This tutorial refers to such lines as "line segments". The shortest distance between a point and a line segment may be the length of the perpendicular connecting the point and the line or it may be the distance from either the start or end of the line.

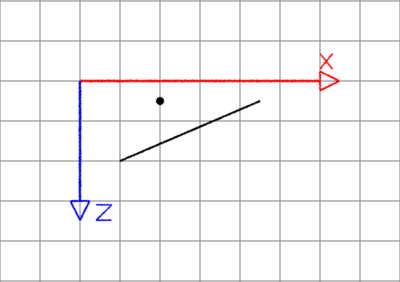
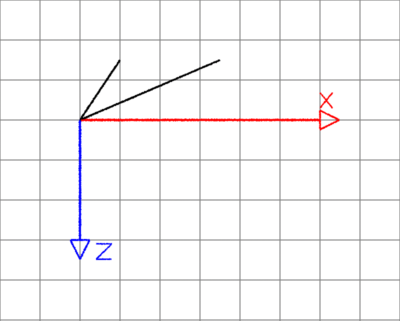
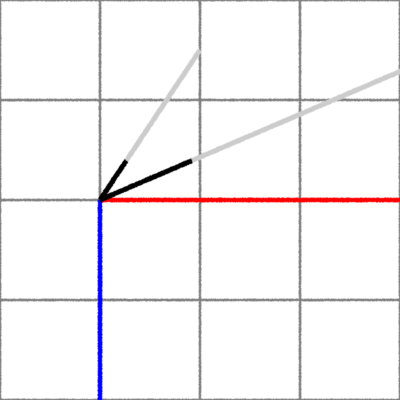
For example, point P in figure 1B is bounded by the two gray perpendicular lines and as such the shortest distance is the length of the perpendicular green line d2. The points in figures 1A and 1C are outside their respective starting and ending perpendiculars and consequently the shortest distance must be calculated from either the start or the end of the line segment.

Figure 1

To B or not to B?

The python procedure presented in listing 1 primarily depends on the use the vector dot product to determine if the shortest distance is d2, case B, or d1 or d3 shown cases A and C. The procedure pnt2line uses a few vector procs that are implemented in,
    vectors.py.
Figures 4 to 8 illustrate each calculation performed by pnt2line. Consider the point and the line segment shown in figurs 2 and 3.

Coordinate Inputs

    Line:

    start (1, 0, 2) end (4.5, 0, 0.5)

    pnt (2, 0, 0.5)

Figure 2

The Y coordinates of the line and point are zero and as such both lie on the XZ plane.

Figure 3

Step 1

Convert the line and point to vectors. The coordinates of the vector representing the point are relative to the start of the line.

    line_vec = vector(start, end) # (3.5, 0, -1.5)
    pnt_vec = vector(start, pnt)  # (1, 0, -1.5)

Figure 4

Step 2

Scale both vectors by the length of the line.

    line_len = length(line_vec)                    # 3.808
    line_unitvec = unit(line_vec)                  # (0.919, 0.0, -0.394)
    pnt_vec_scaled = scale(pnt_vec, 1.0/line_len)  # (0.263, 0.0, -0.393)

Figure 5

Step 3

Calculate the dot product of the scaled vectors. The value corresponds to the distance, shown in black, along the unit vector to the perpendicular, shown in green.

    t = dot(line_unitvec, pnt_vec_scaled)  # 0.397

Figure 6

Step 4

Clamp 't' to the range 0 to 1. Scale the line vector by 't' to find the nearest location, shown in green, to the end of the point vector. Calculate the distance from the nearest location to the end of the point vector.

    if t < 0.0:
        t = 0.0
    elif t > 1.0:
        t = 1.0
    nearest = scale(line_vec, t)      # (1.388, 0.0, -0.595)
    dist = distance(nearest, pnt_vec) # 0.985

Figure 7

Step 5

Translate the 'nearest' point relative to the start of the line. This ensures its coordinates "match" those of the line.

    nearest = add(nearest, start)  # (2.388, 0.0, 1.405)

Figure 8

Listing 1 (distances.py)

from vectors import *
  
# Given a line with coordinates 'start' and 'end' and the
# coordinates of a point 'pnt' the proc returns the shortest 
# distance from pnt to the line and the coordinates of the 
# nearest point on the line.
#
# 1  Convert the line segment to a vector ('line_vec').
# 2  Create a vector connecting start to pnt ('pnt_vec').
# 3  Find the length of the line vector ('line_len').
# 4  Convert line_vec to a unit vector ('line_unitvec').
# 5  Scale pnt_vec by line_len ('pnt_vec_scaled').
# 6  Get the dot product of line_unitvec and pnt_vec_scaled ('t').
# 7  Ensure t is in the range 0 to 1.
# 8  Use t to get the nearest location on the line to the end
#    of vector pnt_vec_scaled ('nearest').
# 9  Calculate the distance from nearest to pnt_vec_scaled.
# 10 Translate nearest back to the start/end line. 
# Malcolm Kesson 16 Dec 2012
  
def pnt2line(pnt, start, end):
    line_vec = vector(start, end)
    pnt_vec = vector(start, pnt)
    line_len = length(line_vec)
    line_unitvec = unit(line_vec)
    pnt_vec_scaled = scale(pnt_vec, 1.0/line_len)
    t = dot(line_unitvec, pnt_vec_scaled)    
    if t < 0.0:
        t = 0.0
    elif t > 1.0:
        t = 1.0
    nearest = scale(line_vec, t)
    dist = distance(nearest, pnt_vec)
    nearest = add(nearest, start)
    return (dist, nearest)

Figure 9 shows 150 points in random locations and their "connections" to their nearest location on a line.

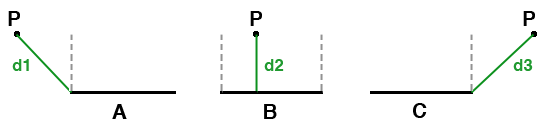
Figure 1