Hilbert Curve
Mel Implementation

return to main index

Introduction

This tutorial follows on from the introduction to Hilbert curves, "Hilbert Curve: Concepts & Implementation". The purpose of this tutorial is to develop examples of Hilbert curves for use with Maya. Figure 1 shows the output of the mel script given in listing 1.

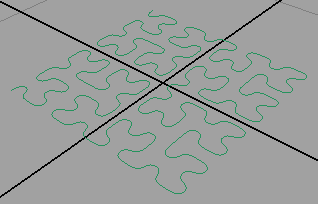
Figure 1

In the hilbert proc the y coordinate is maintained at zero, hence the curve is aligned to the x-z plane. However, some fairly interesting effects can be achieved by assigning a non-zero value to the y coordinate of the control vertices (cv's). The next section explores a few examples of "lofted" Hilbert curves.

Listing 1 (hilbert.mel)

vector $cvs[];
  
global proc hilbert(float $x0, float $y0, float $xi, 
                    float $xj, float $yi, float $yj, int $n)
{
global vector $cvs[];
if($n <= 0)
    {
    float $x = $x0 + ($xi + $yi)/2;
    float $z = $y0 + ($xj + $yj)/2;
    
    // Output the coordinates of the cv
    $cvs[size($cvs)] = <<$x,0,$z>>;
    }
else
    {
    hilbert($x0,            $y0,            $yi/2, $yj/2, $xi/2, $xj/2, $n-1);
    hilbert($x0+$xi/2,      $y0 + $xj/2,    $xi/2, $xj/2, $yi/2, $yj/2, $n-1);
    hilbert($x0+$xi/2+$yi/2,$y0+$xj/2+$yj/2,$xi/2, $xj/2, $yi/2, $yj/2, $n-1);
    hilbert($x0+$xi/2+$yi,  $y0+$xj/2+$yj, -$yi/2,-$yj/2,-$xi/2,-$xj/2, $n-1);
    }
}
  
global proc drawHilbert(int $degree, int $reps)
{
global vector $cvs[];
  
// Cleanup from the previous run
clear $cvs;
  
// Delete curves from prior runs of the script
string $items[] = `ls "curve*"`;
if(size($items) > 0)
    {
    select $items;
    delete;
    }
  
// Begin the Mel curve statement
string $cmd = "curve -d " + $degree + " -periodic 0 ";
  
// Calculate the cv's
hilbert(-0.5, -0.5 , 1.0, 0.0, 0.0, 1.0, $reps);
  
// Copy the cv data
for($n = 0; $n < size($cvs); $n++)
    $cmd += " -p " + $cvs[$n];
  
// Create the curve
eval($cmd);
}
  
drawHilbert 3 4;

Variations of the Hilbert Curve

Setting a value for the y coordinate based on absolute difference between the x and z coordinates of a cv, as shown in the following code snippet, generates a pyramid - figure 2.

if($n <= 0)
    {
    float $x = $x0 + ($xi + $yi)/2;
    float $z = $y0 + ($xj + $yj)/2;
    float $y = 0;
    if(abs($z) > abs($x))
        $y = 0.5 - abs($z);
    else
        $y = 0.5 - abs($x);
    $y *= 2;
  
    // Output the coordinates of the cv
    $cvs[size($cvs)] = <<$x,$y,$z>>;
    }

Figure 2 - Pyramid

The next variation applies a similiar test to the absolute values of x and z but the result is quite different - figure 3.

if($n <= 0)
    {
    float $x = $x0 + ($xi + $yi)/2;
    float $z = $y0 + ($xj + $yj)/2;
    float $y = 0;
    if(abs($z) < abs($x))
        $y = 0.5 - abs($z);
    else
        $y = 0.5 - abs($x);
    $y *= 2;
    // Output the coordinates of the cv
    $cvs[size($cvs)] = <<$x,$y,$z>>;
    }

Figure 3 - "roof"

By setting the y coordinate proportional to the distance of the cv to the origin of the curve a "conical" shape can be produced - figure 4.

if($n <= 0)
    {
    float $x = $x0 + ($xi + $yi)/2;
    float $z = $y0 + ($xj + $yj)/2;
    float $y = 0;
    $y = 0.5 - mag(<<$x,$y,$z>>);
    $y *= 1.5;
    
    // Output the coordinates of the cv
    $cvs[size($cvs)] = <<$x,$y,$z>>;
    }

Figure 4 - Conical