Rsl - Archemedes Spiral

RSL
Archemedes Spiral

Introduction

For a point to be located on an Archemedian spiral it's distance from the center of the spiral (R) must be the same as some percentage (coeff) of it's rotational angle (theta) around the center of the spiral ie.

R = coeff * theta

Naively, it might be considered that all a shader has to do is,
- convert the s,t location of the point being shaded to polar coordinates,
- set a value for coeff,
If the angle of rotation (theta) multiplied by the coeff matches it's radial distance (R) to within a small margin of error then colorize the micro-polygon, say black, otherwise set it to a background color.

Figure 1 shows that this naive approach, listing 1, does not work. The spiral terminates after it's first "turn" - he black line should continue along the full spiral shown in blue.

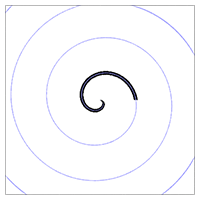
Figure 1 - woops

Listing 1 - woops.sl

surface 
woops(color bakcolor = 1;
      color pencolor = 0;
      float coeff = 0.03;
      float tolerance = 0.01)
{
float     R, theta;
  
// Convert the s,t location of the shading point 
// to polar coordinates.
float   xdiff = s - 0.5, ydiff = t - 0.5;
R = sqrt(xdiff * xdiff + ydiff * ydiff);
theta = atan(ydiff, xdiff); // -PI to PI radians
if(theta < 0.0)
    theta += 2 * PI;        // 0 to 2PI radians
  
Oi = Os;
// Check if we are close enough...
if( abs(R - coeff * theta) < tolerance)
    Ci = Oi * Cs * pencolor;
else
    Ci = Oi * Cs * bakcolor;
}

Clearly what the shader fails to take into account is the number of turns or cyles of the spiral. In other words the rotational angle calculated by the conversion to polar coordinates only go from 0 to 2PI (0 to 360 degrees) when in fact they should go from zeor to 2PI * turns, say, 0 to 1080 degrees!

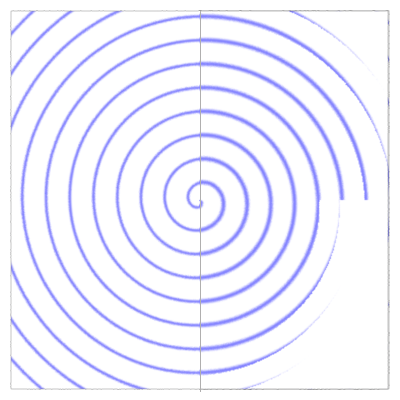
Listing 2 provides the code for a shader that will draw a full spiral. However, becuase of the simple antialiasing that it uses, the "blur" parameter may need to be adjusted in order to avoid the rendering artifacts shown on the right of figure 2.

Figure 2

Listing 2 - a_spiral.sl

surface a_spiral(color bakcolor = 1;
                 color pencolor = 0;
                 float center_s = 0.5;
                 float center_t = 0.5;
                 float coeff = 0.03; /* smaller values give more turns */
                 float blur = 0.03      /* adjust to avoid artifacts */)
{
color    surfcolor = 1;
float     R, theta;
  
// Convert the s,t location of the shading point to polar coordinates.
float   xdiff = s - center_s, ydiff = t - center_t;
R = sqrt(xdiff * xdiff + ydiff * ydiff);
theta = atan(ydiff, xdiff); // -PI to PI radians
if(theta < 0.0)
    theta += 2 * PI;        // 0 to 2PI radians
  
// Remap theta from 0 to 2PI radians to the range 0.0 to 1.0
float   percent_theta = theta/(2 * PI);
  
// The unitRadius defines the maximum size of the spiral when
// theta is 2PI radians ie. 360 degrees. Unless it's size is 
// tweaked by the blur factor "cycles" increments before theta
// reaches 2PI and the spiral will have breaks ie. artifacts.
float     unitRadius = coeff * 2 * PI + mix(-blur,blur,percent_theta);
  
// If the radial distance of shading point is, say, 1.5 the unit
// radius then it is somewhere within the 2nd "turn" of the spiral.
float     turns = floor(R/unitRadius);
  
theta = theta + turns * 2 * PI;
  
// Use "turns" to calculate the full rotational angle. 
theta = coeff * theta;
  
// Determine how close the shading point is to the "true" spiral
float blend = smoothstep(0, blur, abs(theta - R));
  
surfcolor = mix(pencolor, bakcolor, blend);
  
// Uncomment the next couple of lines if you wish to view the 
// unitRadius. Because it is calculated with the addition of a
// value based on blur and theta the unitRadius defined a circle
// with a gap, the size of which is twice the width of blur.
/*
if(abs(R - unitRadius) < 0.002)
    surfcolor = color(1,0,0);
*/
Oi = Os;
Ci = Oi * Cs * surfcolor;
}

RSL Archemedes Spiral

Introduction

RSL
Archemedes Spiral