A Basic Surface Shader
Prior to shading an object a RenderMan complient renderer subdivides the surface of an object into mirco-polygons. The role of a surface shader is to determine the apparent surface opacity and color of each micro-polygon. The first set of shaders in this section are based on Cutter's "Constant" template surface shader.
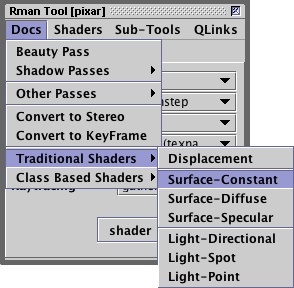
To create a new shader document
select either "Diffuse" or "Constant"
Although a constant shader does not consider the effect of lighting it is, nonetheless, a very good starting point for learning about shader writing.
The Constant Color Shader
/* Shader description goes here */
surface
constant_test(float Kfb = 1 /* fake brightness */)
{
color surfcolor = 1;
/* STEP 1 - set the apparent surface opacity */
Oi = Os;
/* STEP 2 - calculate the apparent surface color */
Ci = Oi * Cs * surfcolor * Kfb;
}
|
In STEP 1 the apparent surface opacity is
assigned the same value of the true surface opacity. In other words, this shader ensures
a surface will conform exactly to the value of the Opacity statement in the rib file.
Opacity 1 1 1 # this will define the value of "Os"
Color 1 1 1 # this will define the value of "Cs"
Surface "constant_test" "Kfd" 1
Polygon "P" [data....]
The global variables that defines the apparent surface opacity and the true surface
opacity are Oi and Os. Hence, the assignment,
Oi = Os;
ensures that nothing fancy is being done to the opacity of an object.
In STEP 2 the apparent surface color (Ci) is assigned the
value of the true surface color (Cs) tinted by an internally defined variable
called surfcolor.
Colors are "combined" by their red, green and blue components being multiplied together.
Color multiplication, filters (or tints) one color by another color. Because
surfcolor is white ie. its rgb components are all equal to 1.0, it has no effect on the resulting color. In later examples,
surfcolor will have a noticable effect on the final apparent color of a surface.
The multiplication by the apparent surface opacity (Oi) ensures the
resulting color of each micro-polygon is pre-multiplied by its opacity. This
enables the renderer to correctly composite the micro-polygons of foreground surfaces
over micro-polygons of surfaces in the background.