QuadTree
Blobby Geometry


return to main index


Introduction

This tutorial demonstrates how sub-classes of the Node and QuadTree classes introduced in QuadTree: Python can be used to explore some aspects of blobby geometry. An example, of the interaction of positive and negative "blobby circles" is shown in figure 1. The quadtree (2D) technique shown in this tutorial is intended to be an introduction to 3D methods that use octrees.



Figure 1


Similar, but non-interacting, circles produced by cquadtree.py and visualized using RenderMan are shown in figure 2. For another tutorial that deals with blobby shapes refer to RSL: Blobby Effects



Figure 2



The Interaction of Positive & Negative Fields

Unlike figure 2 where the small green squares trace the circumferences of two circles, those in figure 1 mark the boundary of two "clouds" of (scalar) values such that their combined values are 0.5 or greater. The two dark red dots in figure 1 mark the centers of two radial fields of values that have a maximum value of 1.0 (positive field) and -1.0 (negative field) at the red dots and at a fixed radial distance have a value 0.0.

Figure 3 shows the positive and negative fields visualized as a grayscale. The green line marks locations where the grayscale value is 0.5.



Figure 3


Another way of visualizing a scalar field is to represent its values as heights - figure 4.



Figure 4


Radial Distances and Field Values

The code presented later in this tutorial calculates the (scalar) field value at a point in space according to its distance from one or more blobby geometries such as circles and lines. The formula for converting a distance to a field value in the range 0 to 1 is taken from the research of Geoff Wyvill and Craig McPhetters "Data Structure for Soft Objects", The Visual Computer, Vol 2 1986. Wyvill calls his geometries Soft Objects. The terminology used in this tutorial follows Pixar's RenderMan and refers to Wyvill's soft objects as Blobby Geometries.

Others, such as Nishimura and Blinn name similar objects as Metaballs. For example, Nishimura et al "Object Modelling by Distribution Function and a Method of Image Generation", The Transactions of the Institute of Electronics and Communication Engineers of Japan, 1985, Vol. J68-D, Part 4, pp. 718-725, in Japanese, translated into English by Takao Fujuwara.


Wyvill & McPhetters

This tutorial, in an attempt to be as pictorial as possible, will not delve into the mathematics of their "field function". Different researchers have different ways of using distances to calculate a scalar field. Their technique is used here because it does not rely on ray tracing. Their technique is relatively fast and generates smooth iso-contours in 2D and smooth iso-surfaces in 3D. The prefix "iso" simply means "equal", as in a contour or a surface sharing the same field value. The code that performs the calculation is shown next.


Listing 1 (see blobby_quadtree.py)

# Given the distance (squared) to the center of a circle or the
# shortest distance to a line and the radius of influence (squared) 
# the proc returns a field value in the range 0 to 1.
def fieldvalue(d2, r2):
    if d2 >= r2:
        return 0.0
    d4 = d2 * d2
    d6 = d2 * d4
    r4 = r2 * r2
    r6 = r2 * r4
    return (-0.44444 * d6/r6 + 1.88889 * d4/r4 + -2.44444 * d2/r2 + 1)


Avoiding Sampling Errors

A quadtree subdivides a rectangle only if it detects that any of its four (children) sub-rectangles spans an iso-contour. Field values at each vertex might be calculated and if there is a mixture of values greater and smaller than 0.5 then the rectangle must be spanning an iso-contour (figure 5).


Figure 5


Relying solely on vertex sampling will also fail if the iso-contour is completely contained within the rectangle (figure 6) or if the iso-contour only passes through an edge (figure 7).


Figure 6


Figure 7


Figure 8 visualizes a quadtree that has relied solely on vertex sampling. Figure 9 demonstrates the use of a preliminary test that determines if the center of any of the blobby circles are with a sub-rectangle. Figure 10 shows the effect of applying a third test to determines if any of the edges of a sub-rectangle are within a certain distance of the center of any blobby circle. The tests are applied in the following order, from computationally cheapest to most expensive.

A rectangle is forced to subdivide if,
    it contains the center of a blobby circle,
    the distance for any edge to a blobby circle is less than the radius/2,
    its vertices have a mixture of field values < 0.5 and >= 0.5


Figure 8


Figure 9


Figure 10


Because adjacent sub-rectangles share vertices their field values are stored in a dictionary that acts as a lookup table - see BlobbyNode.vertLUT. Previously calculated field values can then be reused by rectangles that share a vertex. The impact on memory useage is well worth the extra efficiency. For example, the quadtree for figure 11 was calculated in 400 milliseconds (Mac 2.66 GHz laptop). It reused 19,731 of the total 26,612 field value calculations. The same quadtree took 975 milliseconds without the use of the lookup table.



Figure 11


The code in listing 2 should be saved in the same directory as quadtree.py, vectors.py and distances.py.

Open blobby_quadtree.py with Cutter and look for the following comment,
### EDIT PATH ###
Edit the path to the location where the archive rib will be saved. Use the keyboard shortcut control+e or alt+e to execute the script.



Listing 2 (blobby_quadtree.py)

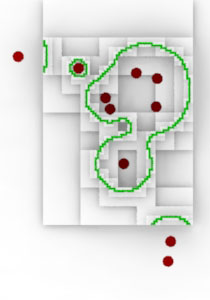
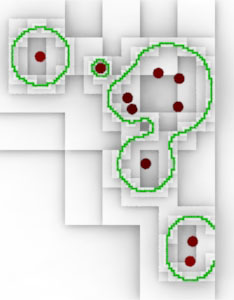
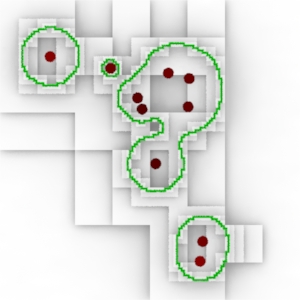
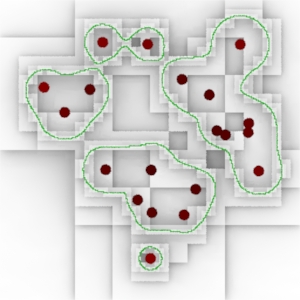
# blobby_quadtree.py
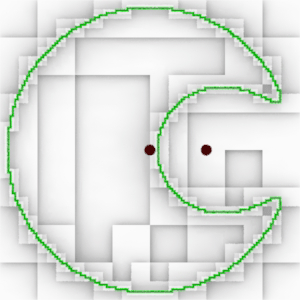
# A quadtree that finds an implicit field that outlines a
# soft (blobby) circles. The field values are calculated using
# Geoff Wyvill and Craig McPhetters method. See,
#     "Data Structure for Soft Objects", The Visual Computer,
#      Vol 2 1986, (page 228)
# Malcolm Kesson Dec 19 2012
from quadtree import Node, QuadTree
import random, time
from distances import pnt2line
  
#____UTILITY PROCS_______________________________________
# Returns the length of a vector "connecting" p0 to p1.
# To avoid using the sqrt() function the return value is
# the length squared.
def dist_sqrd(p0, p1):
    x,y,z = p0
    X,Y,Z = p1
    i,j,k = (X - x, Y - y, Z - z)
    return i * i + j * j + k * k
#_______________________________________________________
def getedges(rect):
    x0,z0,x1,z1 = rect
    edges = ( ((x0,0,z0),(x1,0,z0)), # top
              ((x1,0,z0),(x1,0,z1)), # right
              ((x1,0,z1),(x0,0,z1)), # bottom
              ((x0,0,z1),(x0,0,z0))) # left
    return edges
#_______________________________________________________
# Given the distance (squared) to the center of a circle
# and its radius of influence (squared) the proc returns a 
# (Wyvill) implicit field value in the range 0 to 1.
def fieldvalue(d2, r2):
    if d2 >= r2:
        return 0.0
    d4 = d2 * d2
    d6 = d2 * d4
    r4 = r2 * r2
    r6 = r2 * r4
    return (-0.44444 * d6/r6 + 1.88889 * d4/r4 + -2.44444 * d2/r2 + 1)
#_______________________________________________________
# Returns a string containing the rib statement for a
# four sided polygon positioned at height "y".
def RiPolygon(rect, y):    
    x0,z0,x1,z1 = rect
    verts = []
    verts.append(' %1.3f %1.3f %1.3f' % (x0,y,z0))
    verts.append(' %1.3f %1.3f %1.3f' % (x0,y,z1))
    verts.append(' %1.3f %1.3f %1.3f' % (x1,y,z1))
    verts.append(' %1.3f %1.3f %1.3f' % (x1,y,z0))
    rib =  '\tPolygon "P" ['
    rib += ''.join(verts)
    rib += ']\n'
    return rib
#_______________________________________________________
                
class BlobbyNode(Node):
    verthits = 0
    nonverthits = 0
    vertLUT = {}
    #_______________________________________________________
    # Overrides the base class method.
    # Ensures Node.subdivide() uses instances of our custom 
    # class rather than instances of the base Node class.
    def getinstance(self,rect):
        return BlobbyNode(self,rect)
    #_______________________________________________________
    # Overrides the base class method.
    # Tests: 
    # 1  if the 'rect' contains the center of any blobby circle,
    # 2  if any edges are within half the radius of any circles, 
    # 3  if any vertices span the (blobby) iso-surface.
    # To avoid repeated vertex calculations field values are cached
    # in a lookup table - BlobbyNode.vertLUT
    def spans_feature(self, rect):
        x0,z0,x1,z1 = rect
        size = x1 - x0
        if size > Node.minsize:
            # Cheap test    
            for circle in BlobbyQuadTree.circles:
                pol,rad,x,y,z = circle
                if self.contains(x,z):
                    return True
            # Not so cheap
            for circle in BlobbyQuadTree.circles:
                pol,rad,x,y,z = circle
                if self.depth < 4:# the parent node
                    edges = getedges(rect)
                    for edge in edges:
                        dist,loc = pnt2line( (x,0,z), edge[0], edge[1] )
                        if dist <= rad/2:
                            return True
  
        verts = [(x0,0,z0),(x0,0,z1),(x1,0,z1),(x1,0,z0)]
        span = 0
        # Expensive test, hence the use of a cache
        for vert in verts:
            if self.vertLUT.has_key(vert):
                fv = BlobbyNode.vertLUT[vert]
                BlobbyNode.verthits += 1
            else:
                BlobbyNode.nonverthits += 1
                fv = 0
                for circle in BlobbyQuadTree.circles:
                    pol,rad,x,y,z = circle
                    rad_influ_sqrd = rad * rad
                    center = (x,y,z)
                    dist = dist_sqrd(vert, center)
                    field = fieldvalue(dist, rad_influ_sqrd)
                    if pol == BlobbyQuadTree.POSITIVE:
                        fv += field
                    else:
                        fv -= field
            BlobbyNode.vertLUT[vert] = fv            
            if fv >= BlobbyQuadTree.blobby_level:
                span += 1
        if span > 0 and span < 4:
            return True    
        return False        
     
class BlobbyQuadTree(QuadTree):
    POSITIVE = 1
    NEGATIVE = -1
    circles = []   # list of tuples (polarity, radius of influence,x,y,z)
    blobby_level = 0.5
    #_______________________________________________________
    def __init__(self, rootnode, minrect, circles):
        BlobbyQuadTree.circles = circles
        QuadTree.__init__(self, rootnode, minrect)
    
if __name__=="__main__":
    rootrect = [-2.0, -2.0, 2.0, 2.0]
    resolution = 0.02
    circles = []
    random.seed(1)
    for n in range(20):
        p = BlobbyQuadTree.POSITIVE
        if p < random.random():
            p = BlobbyQuadTree.NEGATIVE
        r = random.uniform(0.2, 0.8)
        x = random.uniform(-1.5, 1.5)
        z = random.uniform(-1.5, 1.5)
        circles.append( (p,r,x,0,z) )
    #circles = [(1,3.8,0,0,0),(-1, 1.3,0.75,0,0)]
    begintime = time.time()
    rootnode = BlobbyNode(None, rootrect)
    tree = BlobbyQuadTree(rootnode, resolution, circles)
    endtime = time.time()
    print (endtime - begintime) * 1000
  
    # Output RenderMan polygons for each node
    ribpath = 'FULL_PATH_TO_ARCHIVE/nodes.rib' ### EDIT PATH ###
    f = open(ribpath,'w')
    f.write('AttributeBegin\n')
    for node in BlobbyQuadTree.allnodes:
        height = node.depth * 0.1
        if node.depth == BlobbyQuadTree.maxdepth:
            f.write('\tColor 0 .5 0\n')
        else:
            f.write('\tColor 1 1 1\n')
        f.write(RiPolygon(node.rect, height))
    f.write('AttributeEnd\n')
    f.write('Color 1 0 0\n')
    for c in circles:
        f.write('Points "P" [%1.3f 1 %1.3f] "constantwidth" [0.15]\n' % (c[2],c[4] ) )
    f.close()
    print('Wrote %d polygons' % len(BlobbyQuadTree.allnodes))
    print('vert hits %d misses %d' % (BlobbyNode.verthits,BlobbyNode.nonverthits))



© 2002- Malcolm Kesson. All rights reserved.